Triplet Loss: Vector Collapse Prevention

Triplet Loss is one of the most widely known loss functions in similarity learning. If you want to deep-dive into the details of its implementations and advantages, you can read this previous tutorial.

Despite its popularity and success, Triplet Loss suffers from what is called vector collapsing, a common problem in similarity learning. A collapse of the vector space is the state when an encoder satisfies the loss function by simply mapping all input samples onto a single point (or a very small area) in the vector space without truly learning useful features for the task. When you look at the graph of the loss in such a case, you are expected to see a decrease in the loss value for a small number of steps followed by a sudden drop to a steady value which is very close to the margin value. This may be observed in the batch-hard strategy, which is usually preferred because it is less greedy and thus performs better than the batch-all strategy if you can avoid the vector space collapse problem.

Collapsed model loss	Fixed loss

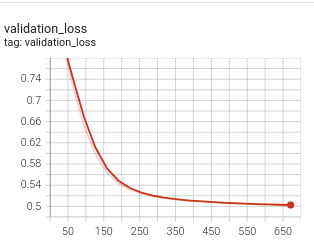
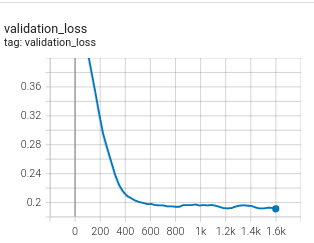
Let’s see why it happens.

The batch-hard strategy computes the triplet loss as the absolute difference of distances between the hardest anchor-positive and hardest anchor-negative pairs summed with the margin value. Hardest anchor-positive pairs are the ones that have the maximum distance, while the hardest anchor-negatives pairs are the ones that have the minimum distance.

In its basic form, this value is calculated as in the following:

triplet_loss = F.relu(
    hardest_positive_dists - hardest_negative_dists
    + self._margin
)

The problem with this equation is that if the encoder outputs the same vector for all the samples, then the loss value will be equal to the margin value, and it will no longer improve.

To prevent it from being stuck to the margin value, Quaterion adds a small trick to scale the difference by the mean of the hardest anchor-negative distances, and the code becomes:

triplet_loss = F.relu(
    (hardest_positive_dists - hardest_negative_dists)
    / hardest_negative_dists.mean()
    + self._margin
)

This division trick introduces an extra penalty in the case of large distances between the hardest anchor-negative pairs, and the model can continue to improve to achieve a smaller loss than the margin value, which is the case that we observed in our experiments.